Οι κεντρογραφικές τεχνικές αποτελούν τις βασικές τεχνικές περιγραφικής στατιστικής της χωρικής κατανομής. Ο πιο απλός περιγραφικός δείκτης μιας κατανομής είναι ο χωρικός μέσος (mean center). Ουσιαστικά πρόκειται για τον μέσο όρο των συντεταγμένων Χ,Υ μιας σημειακής κατανομής. Συχνά αποκαλείται και κεντροειδές.
Δίνεται από τον τύπο:
\[{x}=\frac{\sum\limits_{i=1}^n{x_i}}{n}, {y}=\frac{\sum\limits_{i=1}^n{y_i}}{n}\]
όπου,
\(x,y\) οι συντεταγμένες του χωρικού μέσου δηλαδή ο μέσος όρος των συντεταγμένων \(x_i,y_i\) του πλήθους \(N\) των σημείων της κατανομής. Ταυτόχρονα με τον αριθμητικό χωρικό μέσο, μπορεί να υπολογιστεί ο σταθμισμένος χωρικός μέσος (Weighted Mean Center) όπου ο υπολογισμός γίνεται με το στάθμισμα κάθε συντεταγμένης με μία μεταβλητή π.χ. εισόδημα, εγκληματικότητα, πληθυσμός κτλ.
Δίνεται από τον τύπο:
\[{x}_w=\frac{\sum\limits_{i=1}^n{w_ix_i}}{n},{y}_w=\frac{\sum\limits_{i=1}^n{w_iy_i}}{n}\]
όπου, \(x_w,y_w\) οι συντεταγμένες του σταθμισμένου χωρικού μέσου δηλαδή ο μέσος όρος των διακριτών συντεταγμένων \(x_i,y_i\) του πλήθους \(N\) των σημείων της κατανομής σταθμισμένες με το βάρος \(W_i\) του κάθε σημείου.
Παράλληλα με τον χωρικό μέσο ή τον σταθμισμένο χωρικό μέσο, υπολογίζεται και η τυπική απόσταση (Standard Distance) ως δείκτης μέτρησης του βαθμού συγκέντρωσης ή διασποράς των σημείων γύρω από τον χωρικό (ή σταθμισμένο) μέσο. Αποτέλει ότι και η τυπική απόσταση σε μια μη χωρική κατανομή. Δίνεται από τον τύπο:
\[S_D=\sqrt{\frac{\sum\limits_{i=1}^n(x_i-{x})^2 + \sum\limits_{i=1}^n(y_i-{y})^2}{n}}\]
όπου, \(S_D\) , η τυπική απόσταση, \(x,y\) οι συντεταγμένες του χωρικού μέσου και \(x_i,y_i\) οι συντεταγμένες του κάθε διακριτού σημείου της σημειακής κατανομής.
Κατ’ αντιστοιχία, υπολογίζεται και η σταθμισμένη τυπική απόσταση (weighted standard distance) σε περιπτώσεις που μελετάται η διασπορά σε σχέση με τον σταθμισμένο μέσο όρο.
Δίνεται από τον τύπο:
\[S_{WD}=\sqrt{\frac{\sum\limits_{i=1}^n w_i(x_i-{x})^2 + \sum\limits_{i=1}^n w_i(y_i-{y})^2}{n}}\]
όπου, \(S_{WD}\) , η σταθμισμένη τυπική απόσταση, \(x,y\) οι συντεταγμένες του χωρικού μέσου, \(x_i,y_i\) οι συντεταγμένες του κάθε διακριτού σημείου της σημειακής κατανομής και \(W_i\) τ το αντίστοιχο βάρος τους.
Οι ανωτέρω δείκτες αποκτούν ιδιαίτερη αξία όταν συγκριθούν διαχρονικά.
Ας περιγράψουμε ένα παράδειγμα υπολογισμού των παραπάνω δεικτών με το R. Η σημειακή κατανομή θα αποτελείται από τους οικισμούς του Ν. Θεσπρωτίας και από τον πραγματικό πληθυσμό τους κατά τα έτη 1991 και 2001 για περιπτώσεις υπολογισμού σταθμισμένων δεικτών.
Ο υπολογισμός των δεικτών χωρικής κεντρικότητας στο R γίνεται με την χρήση του πακέτου aspace.
Πριν λοιπόν ξεκινήσουμε πρέπει να εγκαταστήσουμε τα απαραίτητα πακέτα στο R: aspace, maptools, shapefiles, rgdal
Ξεκινήστε το R ως υπερχρήστης (αλλιώς η εγκατάσταση των πακέτων θα αποτύχει) και δώστε τις παρακάτω εντολές
install.packages("aspace")
install.packages("maptools")
install.packages("shapefiles")
install.packages("rgdal")Στην συνέχεια θα σας ζητηθεί να επιλέξετε έναν mirror. Επιλέξτε Greece και συνεχίστε. Επανεκκινήστε το R ως κανονικός πλέον χρήστης και δοκιμάστε να φορτώσετε τα παραπάνω πακέτα με τις εξής εντολές:
library("aspace")
library("maptools")
library("shapefiles")
library("rgdal")την συνέχεια ακολουθεί ο υπολογισμός τον δεικτών (ανατρέξτε στα σχόλια για λεπτομέρειες):
Υπολογισμός του Χωρικού Μέσου των οικισμών του Ν. Θεσπρωτίας:
#ανάγνωση του αρχείου shapefile OIKISMOI
oikismoi <- readShapePoints("OIKISMOI")
#Υπολογισμός του χωρικού μέσου mean_center
mean_centre(id=1, filename="mean.txt", weighted=FALSE, weights=NULL, points=coordinates(oikismoi))
#εξαγωγή σε shapefile
shp <- convert.to.shapefile (data.frame(meanloc), data.frame(meanatt),"id",1)
write.shapefile(shp, "Mean", arcgis=T)
#εγγραφή αρχείου prj για το ΕΓΣΑ '87
cat(yt(proj4string<-("+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs")),file="Mean.prj")Ο Χωρικός Μέσος των οικισμών του Ν. Θεσπρωτίας εντοπίζεται στο σημείο Χ=191482.2, Υ=4381093.
Υπολογισμός του Σταθμισμένου Χωρικού Μέσου για τον πραγματικό πληθυσμό του 1991 των οικισμών του Ν. Θεσπρωτίας:
mean_centre(id=1, filename="mean_PRAG91.txt", weighted=TRUE, weights=oikismoi$POPPRAG199, points=coordinates(oikismoi))
#εξαγωγή σε shapefile
shp <- convert.to.shapefile (data.frame(meanloc), data.frame(meanatt),"id",1)
write.shapefile(shp, "Mean_PRAG1991", arcgis=T)
#εγγραφή αρχείου prj για το ΕΓΣΑ '87
cat(showWKT(proj4string<-("+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs")),file="Mean_PRAG1991.prj")Ο Σταθμισμένος Χωρικός Μέσος των οικισμών του Ν. Θεσπρωτίας για το 2001 εντοπίζεται στο σημείο Χ=187644.1, Υ=4378180.
Υπολογισμός της Σταθμισμένης Τυπικής Απόστασης για τον πραγματικό πληθυσμό του 1991 των οικισμών του Ν. Θεσπρωτίας:
## SDD 1991
calc_sdd(id=1, filename="SDD_PRAG91.txt", centre.xy=NULL, calccentre=TRUE,weighted=TRUE, weights=oikismoi$POPPRAG199,points=coordinates(oikismoi),verbose=TRUE)
shp <- convert.to.shapefile(sddloc,sddatt,"id",5)
write.shapefile(shp, "SDD_1991", arcgis=T)
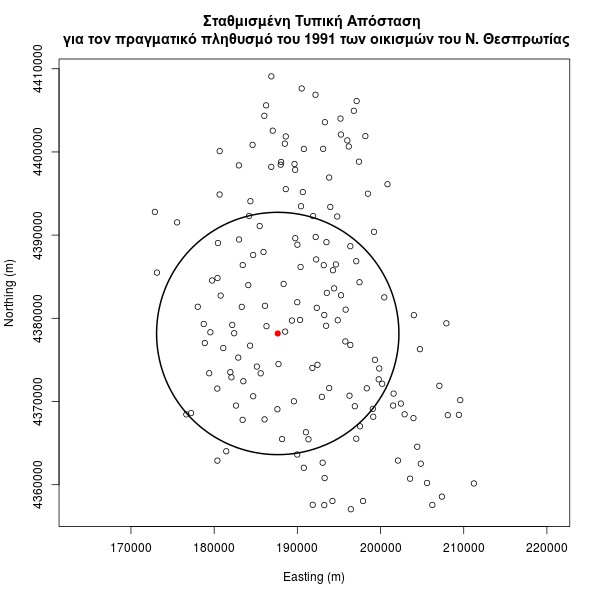
cat(showWKT(proj4string<-("+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs")),file="SDD_1991.prj")Η Σταθμισμένη Τυπική Απόσταση για τον πραγματικό πληθυσμό του 1991 των οικισμών του Ν. Θεσπρωτίας έχει ακτίνα 14563.64μ.
To R δίνει την δυνατότητα στον χρήστη να αποδόσει σε γράφημα τους δείκτες του πακέτου aspace. Στην περίπτωση της Σταθμισμένης Τυπικής Απόστασης η απόδοση γίνεται με την χρήσης της εντολής plot_sdd. Η εντολή plot_sdd αποδίδει την τυπική απόσταση σαν ένα κύκλο με κέντρο τον χωρικό μέσο.
Παρατίθεται η σύνταξη της σχετικής εντολής:
plot_sdd(centre.col='red', titletxt="Σταθμισμένη Τυπική Απόσταση n για τον πραγματικό πληθυσμό του 1991 των οικισμών του Ν. Θεσπρωτίας", jpeg=TRUE)Το αποτέλεσμα είναι το παρακάτω γράφημα:
Υπολογισμός του Σταθμισμένου Χωρικού Μέσου για τον πραγματικό πληθυσμό του 2001 των οικισμών του Ν. Θεσπρωτίας:
mean_centre(id=1, filename="mean_PRAG2001.txt", weighted=TRUE, weights=oikismoi$POPPRAG200, points=coordinates(oikismoi))
#εξαγωγή σε shapefile
shp <- convert.to.shapefile (data.frame(meanloc), data.frame(meanatt),"id",1)
write.shapefile(shp, "Mean_PRAG2001", arcgis=T)
#εγγραφή αρχείου prj για το ΕΓΣΑ '87
cat(showWKT(proj4string<-("+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs")),file="Mean_PRAG2001.prj")Ο Σταθμισμένος Χωρικός Μέσος των οικισμών του Ν. Θεσπρωτίας για το 2001 εντοπίζεται στο σημείο Χ=186711.3, Υ=4377762.
Υπολογισμός της Σταθμισμένης Τυπικής Απόστασης για τον πραγματικό πληθυσμό του 2001 των οικισμών του Ν. Θεσπρωτίας:
## SDD 2001
calc_sdd(id=1, filename="SDD_2001.txt", centre.xy=NULL, calccentre=TRUE,weighted=TRUE, weights=oikismoi$POPPRAG200,points=coordinates(oikismoi),verbose=TRUE)
write.shapefile(shp, "SDD_2001", arcgis=T)
cat(showWKT(proj4string<-("+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs")),file="SDD_2001.prj")Η Σταθμισμένη Τυπική Απόσταση για τον πραγματικό πληθυσμό του 2001 των οικισμών του Ν. Θεσπρωτίας έχει ακτίνα 14019.97μ.
Οι δείκτες είναι πιο αποκαλυπτικοί αν αποδοθούν σε έναν χάρτη.
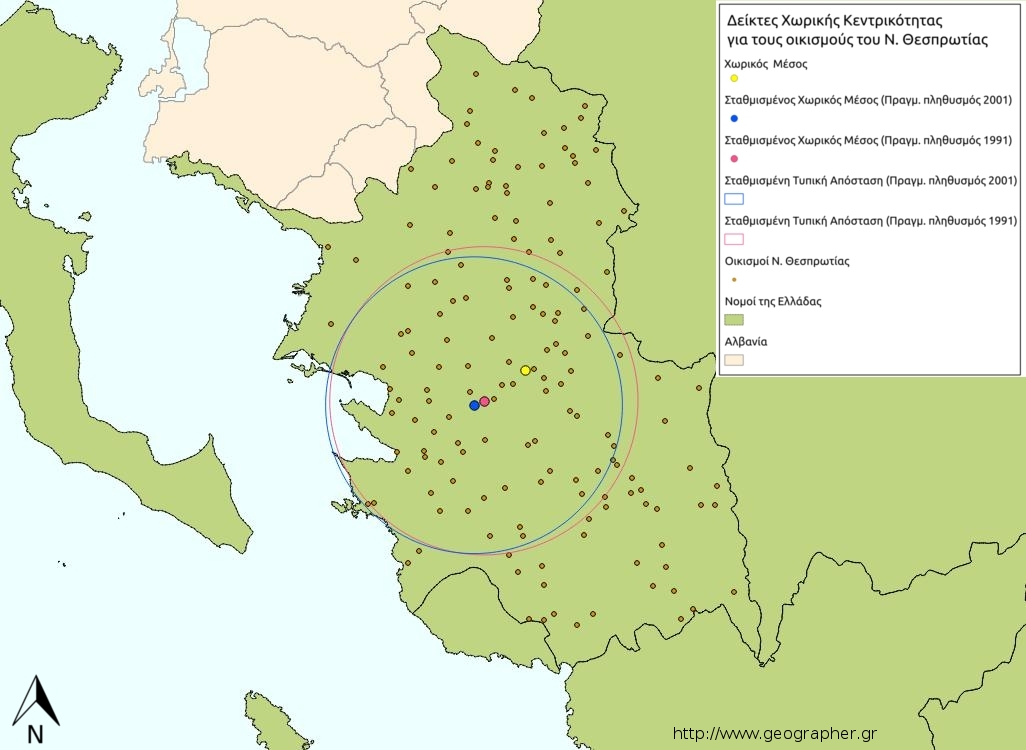
Το πρώτο βασικό συμπέρασμα που διεξάγεται από τον χάρτη είναι ότι οι σταθμισμένοι χωρικοί μέσοι εντοπίζονται ΝΔ από τον χωρικό μέσο προφανώς ως απόρροια της επιρροής του πληθυσμού αστικών κέντρων όπως η Ηγουμενίτσα, η Πέρδικα, το Μαργαρίτι, το Γαρδίκι και η Παραμυθιά.
Όσον αφορά τον σταθμισμένο χωρικό μέσο του πραγματικού πληθυσμού αυτός κινείται διαχρονικά, από το 1991 στο 2001, προς τα Δ-ΝΔ ως αποτέλεσμα της σημαντικής αύξησης του πραγματικού πληθυσμού της Ηγουμενίτσας (+28,00%) και της μείωσης του πληθυσμού των Φιλιατών (-13,00%).
Η σταθμισμένη τυπική απόσταση δεν σημειώνει αξιόλογη μεταβολή παρά μόνο μια μικρή συσπείρωση των τιμών γύρω από τον σταθμισμένο χωρικό μέσο το 2001 σε σχέση με το 1991.
Ανάλογα με τα δεδομένα μας και τον τρόπο προσπέλασης τους ο υπολογισμός των δεικτών μπορεί να γίνει με κλίση του R μέσω python με το πακέτο rpy/rpy2 ή μέσω Grass GIS με το πακέτο spgrass6.
Για παράδειγμα ο υπολογισμός του χωρικού μέσου μπορεί να υπολογιστεί μέσω Python και rpy2 με το παρακάτω script:
import rpy2.robjects as robjects
from rpy2.robjects.packages import importr
r=robjects.r
aspace = importr("aspace")
maptools = importr("maptools")
shapefiles = importr("shapefiles")
rgdal = importr("rgdal")
sp = importr("sp")
shp=maptools.readShapePoints("OIKISMOI")
mean=aspace.mean_centre(id=1, filename="mean.txt", weighted="FALSE", weights="NULL",points=sp.coordinates(shp))
myshp = shapefiles.convert_to_shapefile(r('data.frame(meanatt)'), r('data.frame(meanloc)'), "id",1)
shapefiles.write_shapefile(myshp, "Mean", arcgis="T")
proj4string="+proj=tmerc +lat_0=0 +lon_0=24 +k=0.9996 +x_0=500000 +y_0=0 +ellps=GRS80 +towgs84=-199.87,74.79,246.62,0,0,0,0 +units=m +no_defs"
r.cat(rgdal.showWKT(proj4string, file="Mean.prj"))Η αντίστοιχη διαδικασία μπορεί να εκτελεστεί και μέσω GRASS με την χρήστου του πακέτου [spgrass6](http://cran.r-project.org/web/packages/spgrass6/spgrass6.pdf όπως φαίνεται στο παράδειγμα:
library("aspace")
library("spgrass6")
oikismoi <- readVECT6("OIKISMOI")
mean_centre(id=1, filename="mean.txt", weighted=FALSE, weights=NULL, points=coordinates(oikismoi))
mean_centre <- SpatialPointsDataFrame(coords=data.frame(meanloc[2],meanloc[3]), data=meanatt)
writeVECT6(mean_centre,v.in.ogr_flags=c("o", "overwrite"), "mean_centre")
Comments
comments powered by Disqus